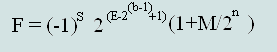 (Formula 1)
(Formula 1)
 Home
Back
Home
Back
Author: Yashkardin Vladimir
www.softelectro.ru
2009-2011
info@softelectro.ru
This standard is designed association IEEE (Institute of Electrical and Electronics Engineers) and is used to represent real numbers (floating point) in binary code. The most used standard for floating point, used by many microprocessor and logic devices and software.
In 2008, the association has released IEEE standard IEEE 754-2008, which included the standard IEEE 754-1985.
The standard contains 23 pages of text in 7 sections and one annex:
Unfortunately, the IEEE has evolved from an international public engineering organization (which it was originally) a trade organization.
This organization owns the copyright to publish the standard IEEE754-1985.
So if you want to read, with the original standard, you have to buy it for around 80 $.
However, Russian law allows me to comment on teaching this standard.
Therefore, the further I'll give an arbitrary presentation of standard and express their opinion about it for training purposes.
Take, for example, the decimal number 155.625
Imagine the number in a normalized exponential form: 1,55625∙10+2=1,55625∙exp10+2
Number 1,55625∙exp10+2 consists of two parts: a mantissa M = 1.55625 and the exponent exp10=+2
If the mantissa is in the range 1 <= M <10, then the number considered to be normalized.
Exhibitor provided the basis of calculation (in this case 10) and order (in this case 2
The order of the exponent can have a negative value, such as the number 0,0155625=1,55625∙exp10-2.
Take, for example, the decimal number 155,625
Imagine the number of denormalized exponential way: 0,155625∙10+3=0,155625∙exp10+3
Number 0,155625∙exp10+3 consists of two parts: a mantissa M = 0,155625 and exponent exp10=+3
If the mantissa is in the range 0,1 <= M <1, then the number is denormalized.
Exhibitor provided the basis of calculation (in this case 10) and order (in this case 3).
The order of the exponent can have a negative value, such as the number 0,0155625=0,155625∙exp10-3.
Our problem is reduced to a decimal floating point numbers in binary floating-point number in exponential normalized form. To do this we expand the given number of binary digits:
155,625 = 1∙27 +0∙26+0∙25+1∙24+1∙23+0∙22+1∙21+1∙20+1∙2-1+0∙2-2+1∙2-3
155,625 =128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125
155,62510 = 10011011,1012 - the number of decimal and binary floating-point
Let the resulting number to the normalized form in decimal and binary system:
1,55625∙exp10+2 = 1,0011011101∙exp2+111
The main application in technology and programming formats were 32 and 64 bits.
For example, in VB using the data types single (32 bit) and double (64 bits).
Consider the transformation of the binary number 10011011.101 format single-precision (32 bit) IEEE Standard 754.
Other formats of the numbers in IEEE 754 is an enlarged copy of the single-precision.
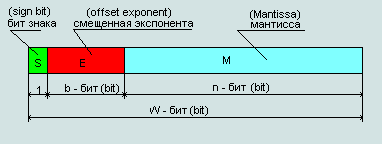
| 1 bit | 8 bit | 23 bit | IEEE 754 |
| 0 | 1000 0110 | 001 1011 1010 0000 0000 0000 | 431BA000 (hex) |
| 0(dec) | 134(dec) | 1810432(dec) | |
| çíàê ÷èñëà | offset exponent | the remainder of the mantissa | number 155.625 in IEEE754 format |
We give a formula for a decimal number from among IEEE754 Single precision:
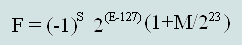 where the F - decimal
where the F - decimal
Check our example:
F =(-1)0∙2(134-127)∙(1+ 1810432 / 223)= 27∙(1+0,2158203125)=128∙1,2158203125=155,625
Fig. 1 Presentation format of the IEEE 754
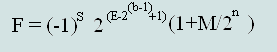 (Formula 1)
(Formula 1)
Using the formula we calculate a formula for finding a decimal to a single (32 bit) and double (64 bits) of accuracy the number recorded in the IEEE 754 standard:
Fig.2 The format of single-precision (single-precision) 32-bit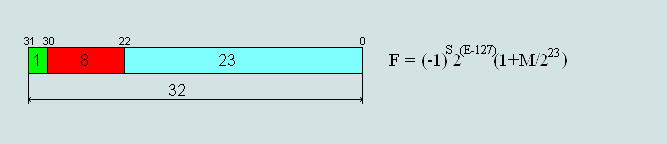
Fig.3 The format of a double-precision (double-precision) 64-bit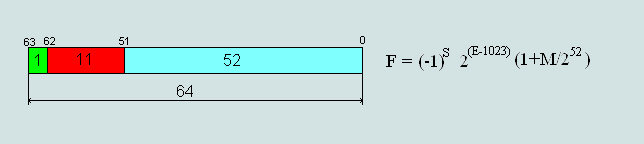
This shows that it is impossible to provide the number of zero or infinity in the given format.
1. Number IEEE754=00 00 00 00hex is the number +0
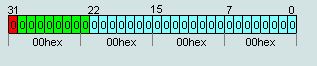
Number IEEE754=80 00 00 00hex is the number -0
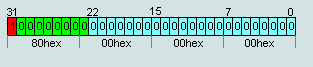
2. Number IEEE754=7F 80 00 00hex is the number +∞
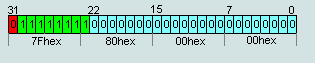
Number IEEE754=FF 80 00 00hex is the number -∞
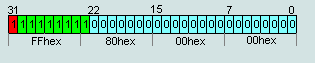
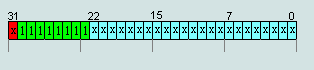
3. Numbers IEEE754=FF (1xxx)X XX XXhex not considered numbers (NAN), unless p.2
Numbers IEEE754=7F (1xxx)X XX XXhex not considered numbers (NAN), unless p.2
The number represented in bits from 0 ... 22 can be any number except 0 (+∞ è -∞ ).
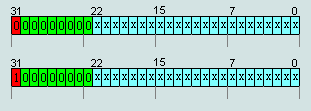
4. Numbers IEEE754=(x000) (0000) (0xxx)X XX XXhex are denormalized numbers, except numbers p.1( -0 and +0)
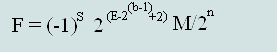 (Formula 2)
(Formula 2)
Given the format of numbers with single precision IEEE Standard 754 can calculate the range for the submission of real numbers in this format. For this we substitute the values of maximum and minimum absolute numbers of IEEE 754 in formula 1 and 2
The minimum number of normalized (absolute)
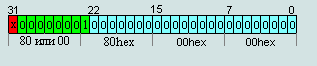
00 80 00 00 = 2-126∙(1+0/223)= 2-126 ≈ 1,17549435∙e-38
80 80 00 00 = -2-126∙(1+0/223)=2-126 ≈ -1,17549435∙e-38
Maximum denormalizovanoe number (absolute)
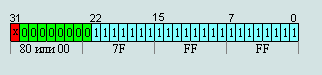
00 7F FF FF = 2-126∙(1-2-23) ≈ 1,17549421∙e-38
80 7F FF FF = -2-126∙(1-2-23) ≈ -1,17549421∙e-38
This shows that the minimum normalized number of borders with a maximum denormalized.
Minimum denormalized number (absolute)
00 00 00 01 = 2-126∙ 2-23= 2-149 ≈ 1,40129846∙e-45
80 00 00 01 = -2-126∙-2-23= 2-149 ≈ -1,40129846∙e-45
This number is bounded by zero.
Maximum number of normalized (absolute)
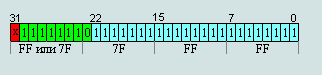
7F 7F FF FF = 2127∙(2-2-23) ≈ 3,40282347∙e+38
FF 7F FF FF = -2127∙(2-2-23) ≈ -3,40282347∙e+38
That number is bordered with infinity.
Ðèñ.The range of numbers the format single-precision (32 bits) represented by the IEEE 754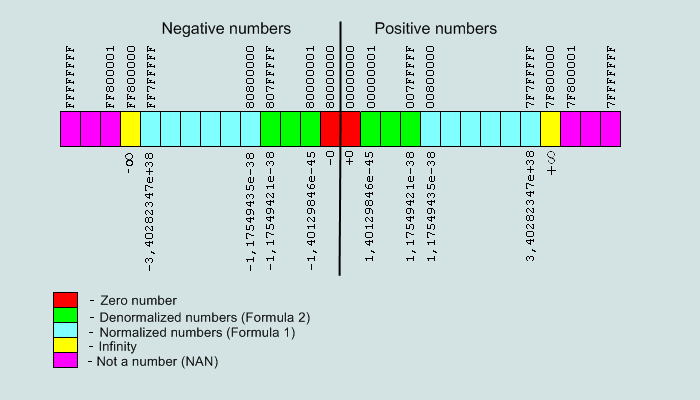
Fig.5 .The range of numbers the format double-precision (32 bits) represented by the IEEE 754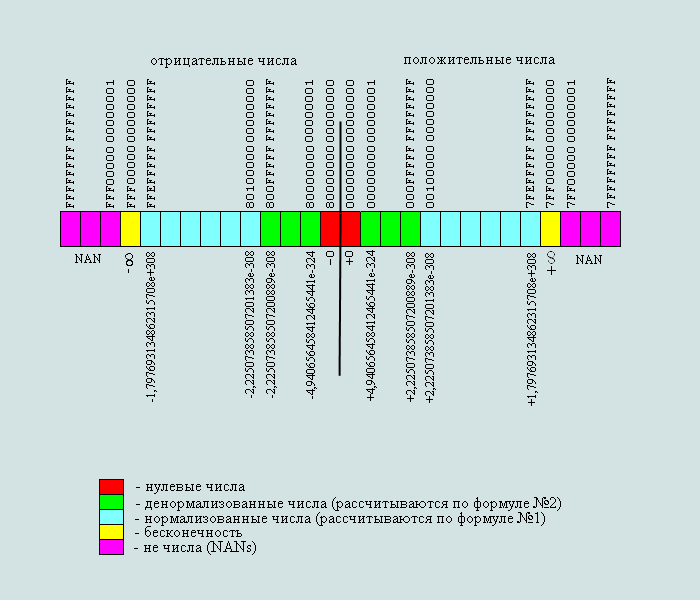
The numbers presented in the format IEEE754 represent a finite set, which displays an infinite set of real numbers. Therefore, the original number can be represented in IEEE754 format with an error.
Fig.6 Error function exactly represent the number of IEEE754 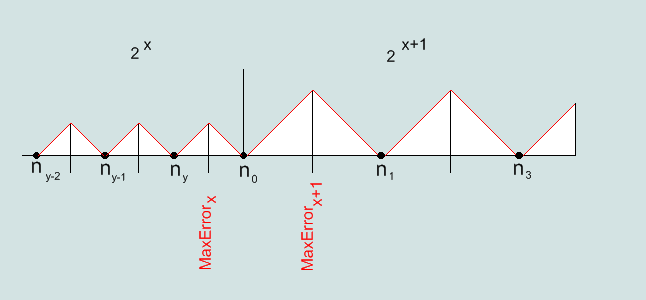
Absolute maximum error for the number in the format IEEE754 is within half a step numbers.
Step numbers doubled with an increase in the exponent of the binary number by one.
That is, the farther away from zero, the greater the step numbers in IEEE754 format on the real axis.
Step number is equal to the lowest level 2(E-22-127)=2(E-149) (Single) è 2(E-51-1023)= 2(E-1074) (Double).
Accordingly, limit the maximum absolute error is 1 / 2 steps of:2(E-150) (Single) è 2(E-1075) (Double).
Relative error in% will be: (2(E-150)/F)*100%(Single) è (2(E-1075)/F)*100% (Double).
The maximum relative error for denormalized numbers (single / double): 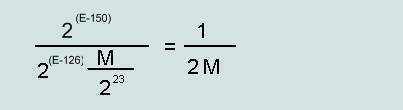
The maximum relative error of the normalized number of (single): 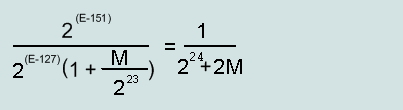
The maximum relative error of the normalized number (double): 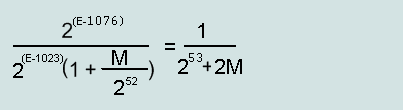
| IEEE754, hex | Number, dec | absolute error, dec | relative , % |
| 00000001 | 2-149 ≈1,401298e-45 | 2-150≈0,700649e-45 | =50 |
| 00000002 | 2-148 ≈2,802597e-45 | 2-150≈0,700649e-45 | =25 |
| 00000032 | ≈7,00649e-44 | 2-150≈0,700649e-45 | =1 |
| 007FFFFF | ≈1,175494e-38 | 2-150≈0,700649e-45 | ≈5,96e-6 |
| 00800001 | ≈1,175494e-38 | 2-149 ≈1,401298e-45 | ≈11,9209e-6 |
| 0DA24260 | ≈1,0e-30 | 2-123 ≈9,4039e-38 | ≈9,4039e-6 |
| 1E3CE508 | ≈1,0e-20 | 2-90 ≈8,0779e-28 | ≈8,0779e-6 |
| 2EDBE6FF | ≈1,0e-10 | 2-57 ≈6,9389e-18 | ≈6,9389e-6 |
| 3F800000 | ≈1,0 | 2-23 ≈1,192e-7 | ≈11,9209e-6 |
| 41200000 | ≈10,0 | 2-20 ≈9,5367e-7 | ≈9,5367e-6 |
| 42C80000 | ≈1,0e+2 | 2-17 ≈7,6294e-6 | ≈7,62939e-6 |
| 501502F9 | ≈1,0e+10 | 210 ≈1,024e+3 | ≈10,24e-6 |
| 60AD78EC | ≈1,0e+20 | 243 ≈8,7961e+12 | ≈8,7961e-6 |
| 7149F2CA | ≈1,0e+30 | 276 ≈7,5558e+22 | ≈7,5558e-6 |
| 7F7FFFFF | ≈+3,40282e+38 | 2104 ≈2,02824e+31 | ≈5,96e-6 |
| IEEE754, hex | Number, dec | absolute error, dec | relative, % |
| 00000000 00000001 | 2-1074 ≈4,940656e-324 | 2-1075≈2,470328e-324 | =50 |
| 00000000 00000002 | 2-1073 ≈9,881313e-324 | 2-1075≈2,470328e-324 | =25 |
| 00000000 00000032 | ≈2,470328e-322 | 2-1075≈2,470328e-324 | =1 |
| 000FFFFF FFFFFFFF | ≈2,225073e-308 | 2-1075≈2,470328e-324 | ≈1,110223e-14 |
| 00100000 00000001 | ≈2,225074e-308 | 2-1074 ≈4,940656e-324 | ≈2,220446e-14 |
| 2B2BFF2E E48E0530 | ≈1,0e-100 | 2-385 ≈1,268971e-116 | ≈1,268971e-14 |
| 3FF00000 00000000 | =1,0 | 2-52 ≈2,220446e-16 | ≈2,220446e-14 |
| 54B249AD 2594C37D | ≈1,0e+100 | 2280 ≈1,942669e+84 | ≈1,942669e-14 |
| 6974E718 D7D7625A | ≈1,0e+200 | 2612 ≈1,699641e+184 | ≈1,699641e-14 |
| 7FEFFFFF FFFFFFFF | ≈1,79769e+308 | 2971 ≈1,99584e+292 | ≈1,110223e-14 |
From the above, given that the bulk of the numbers in IEEE754 format has a stable small relative error:
The maximum possible relative error for the number is Single 2-23*100% =11,920928955078125e-6 %
The maximum possible relative error for the number of Double 2-52*100% =2,2204460492503130808472633361816e-14 %
| Name format | single-precision | double-precision |
| length number, bit | 32 | 64 |
| offset the exponential (E), bits | 8 | 11 |
| the remainder of the mantissa (M), bits | 23 | 52 |
| bias | 127 | 1023 |
| denormalized binary number | (-1)S∙0,M∙exp2-127 ,where M-binary | (-1)S∙0,M∙exp2-1023 ,ãäå M-áèíàðíîå |
| normalized binary number | (-1)S∙1,M∙exp2(E-127) ,where M-binary | (-1)S∙1,M∙exp2(E-1023) ,ãäå M-áèíàðíîå |
| denormalized number of decimal | F =(-1)S∙2(E -126)∙ M/223 | F =(-1)S∙2(E -1022)∙M/252 |
| normalized number of decimal | F =(-1)S∙2(E-127)∙(1+ M/223) | F =(-1)S∙2(E-1023)∙(1+M/252) |
| Abs. max. error number | 2(E-150) | 2(E-1075) |
| Rel. max. error denorms. number | 1/(2M) | 1/(2M) |
| Rel. max. error norms. number | 1/(224+2M) | 1/(253+2M) |
| Min Number | ±2-149≈ ±1,40129846∙e-45 | ±2-1074≈ ± 4,94065646∙e-324 |
| Max Number | ±2127∙(2-2-23) ≈ ± 3,40282347∙e+38 | ±21023∙(2-2-52) ≈ ± 1,79769313∙e+308 |
In presenting the floating-point numbers in IEEE Standard 754 have often rounded numbers. The standard provides four ways to rounding of numbers.
| original number | to the nearest integer | zero | to +∞ | to -∞ |
| 1,33 | 1,3 | 1,3 | 1,4 | 1,3 |
| -1,33 | -1,3 | -1,3 | -1,3 | -1,4 |
| 1,37 | 1,4 | 1,3 | 1,4 | 1,3 |
| -1,37 | -1,4 | -1,3 | -1,3 | -1,4 |
| 1,35 | 1,4 | 1,3 | 1,4 | 1,3 |
| -1,35 | -1,4 | -1,3 | -1,3 | -1,4 |
How is rounding shown in the examples in Table 3. When you convert a number to choose one of the ways of rounding. By default, this is the first way, rounding to the nearest integer. Often in different devices using the second method - rounded to zero. When rounding to zero, simply discard meaningless level numbers, so this is the easiest one in the hardware implementation.
IEEE 754 standard is widely used in engineering and programming.
Most modern microprocessors are manufactured with hardware realization of representations of real variables in the format of IEEE754.
Programming language and the programmer can not change this situation, a repose of a real number in the microprocessor does not exist.
When creating the standard IEEE754-1985 representation of a real variable in the form of 4 or 8 bytes seem very large value, since the amount of RAM MS-DOS was equal to 1 MB.
A program in this system could be used only 0.64 MB.
For modern operating systems the size of 8 bytes is null and void, nevertheless the variables in most microprocessors continue to be in the format IEEE754-1985.
Consider the error computing, caused by the use of numbers in the format of IEEE754
This error is always present in computer calculations.
The reason for its occurrence is described in paragraph 7.4.
-6 for double 10-14
The absolute errors can be significant, as for single 1031 and for double 10292,that may cause problems with calculations.
//Example 1. Error due to the precision of numbers in IEEE754 format
#include "stdio.h"
int
main(int argc, char *argv[])
{
float a, b, f;
a=123456789;
b=123456788;
f=a-b;
printf("Result: %f\n", f);
return 0;
}
Result: 8.000000 (The answer should be 1.000000)
If the sample count on the paper, the answer is 1. Absolute error is +7.
Why get the wrong answer?
Number 123456789 in the single = 4CEB79A3hex (ieee) = 123456792 (dec) absolute error reporting is +3
Number 123456788 in the single = 4CEB79A2hex (ieee) = 123456784 (dec) absolute error reporting is -4
Relative error in the initial numbers of approximately 3,24 e-6%
As a result, one operation relative error of the result was 800%, ie increased by 2,5 e +8 times.
This is what I call"A dangerous reduction", ie catastrophic decrease of accuracy in the operation where the absolute value of the result is much smaller than any of the input variables.
In fact, the error precision of the representation of the most innocuous in computer calculations, and usually many programmers are not paying any attention. Nevertheless, they you can be very frustrating.
These errors are caused by the fact that the original number submitted in the format of single and double in a format not usually equal to each other.
For example: the original number 123456789,123456789
Single: 4CEB79A3 = +123456792,0 (dec)
Double: 419D6F34547E6B75 = +123456789,12345679104328155517578125
The difference between Single and Double amount: 2,87654320895671844482421875
Private Sub Command1_Click()
Dim a As Single
Dim b As Double
Dim c As Double
a = 123456789.123457
b = 123456789.123457
c = a - b
Text1.Text = c
End Sub
The result: 2.87654320895672 (should be 0)
Relative error of the result is:∞ (infinity)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 123456789.123457
b = 123456789.123457
c = a - b
Text1.Text = c
End Sub
Result: 0.0
Therefore, variables and intermediate results of computations to be brought to the same data type. Pay attention to the fact that not enough just to bring all the original data to a single type.
Necessary to bring the results of intermediate operations to the same type.
Here is an example of an error in the intermediate result:
'Example 1 error in the intermediate data in VB (Visual Studio)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 1
b = 3
c = a / b
c = c - 1 / 3
Text1.Text = c
End Sub
Result: 9,934108 E-09 (Must be 0.0)
Here the error arises because the intermediate result of 1 / 3 in the line c = c-1 / 3 will be of type double, not single.
To get rid of the error you have to give an intermediate result to the type of single operator using cast CSng.
'Example 2 The intermediate data to VB (Visual Studio)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 1
b = 3
c = a / b
c = c - CSng(1 / 3)
Text1.Text = c
End Sub
Result: 0.0
An example of bringing data type for GNU C, sent by Gregory Sitkarevym:
//Option 1 is not listed with an intermediate result:
#include "stdafx.h"
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
int
main(int argc, char *argv[])
{
float a, b, c, d;
a = 1.0;
b = 3.0;
c = a / b;
d = (c - 1.0/3.0) * 1.0e9;//the result of dividing 1 / 3 has a double type
printf("Result: %f\n", d);
return 0;
}
Result: 9.934108 (Must be 0.0)
//Option 2 with the above intermediate results:
#include "stdafx.h"
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
int
main(int argc, char *argv[])
{
float a, b, c, d;
a = 1.0;
b = 3.0;
c = a / b;
d = (c - 1.0f/3.0f) * 1.0e9f;//the result of dividing 1 / 3 cast to float
printf("Result: %f\n", d);
return 0;
}
Result: 0.0
In the second version you can see that the division of the constants in the intermediate result is given to the type of "float" (single precision in C).
These options were compiled and executed using the "GNU C".
If you compile and execute the above options are shown on the VC + + (Visual Studio), the results would be reversed.
That is, option 2 would be the result of -9.934108, and option 1 Result: 0.000000.
Hence it can be disappointing conclusion that the result of calculations may depend on the type and version of the compiler.
In this case, we can assume that the VC + + compiler automatically gives the types of variables, and the attempt to forcibly bring the same type fails.
If Option 1 (without the cast) to meet with variable double-precision (double), then the error will not bring data and Result = 0.000000
So in most cases to get rid of the cast data is simply to use the data type double and forget about the type of single (float).
Computational errors caused by not bringing the type of data I call the "Wild errors" as they relate to the ignorance of the standards and the theory of programming (ie, with poor basic education)
1. addition with the same number (the error shift = 0.0).
2. addition to the number of smaller 2-fold (error = shift - 0.00390625).
3. addition with a smaller number of 223 times (error shift = - 0.007812).
4. addition with a smaller number of 224 times (error shift= - 0.007812).
As can be seen from the above examples shift error occurs if the initial normalized numbers are different exponent.
If the numbers differ by more than 2 23 (for single) and 2 52 (for double), then addition and subtraction between these numbers are not possible.
Maximum relative error result of the operation is about 5,96 e-6%, which does not exceed a relative error of representation of the number (p.9.1).
Although the relative error here is all right, there are other problems.
First, work with numbers only in a narrow range of the real axis, where the mantissa intersect.
Secondly, for each source of the limit of a loop called "Cyclic hole" .
Let me explain, if there is a cycle in which the original number is added to the sum, there is a numerical limit on the amount for this number.
That is, the amount reaching a certain size ceases to increase by adding it to the original number.
Here is an example of a cyclic holes in the automatic control system:
There is a pharmaceutical plant producing tablets weighing 10 mg.
Consisting of: forming machine, storage tank of 500 kg, packaging machines, automatic control system.
Molding machine feeds into the bunker on 10 tablets at a time.
Filling machine takes one pill.
The automatic control system takes into account the tablets received in the hopper of the molding machine and taken out of the bunker packaging machines.
That is, there is a program that shows the filling hopper production in kg.
When in the bunker will be over 500 kg product molding machine stands on a break, it includes the code in the bunker will be 200 kg of product.
Filling machine to stop if the bunker is less than 10 pounds and will start when the bunker will be over 100 kg product.
Both cars can stop from time to serve, not dependent on each other (thanks to the bunker).
Here is an example of a cyclic holes in the automatic control system:
There is a pharmaceutical plant producing tablets weighing 10 mg.
Consisting of: forming machine, storage tank of 500 kg, packaging machines, as you know, it works in an endless loop.
Suppose one day filling machine stood too long and a bunker filled with up to 300 kg.
What happens after I turn it on?
Private Sub Command1_Click()
Dim a As Single 'tablet weight in kg
Dim c As Single 'product in the hopper in kg
Dim n As Long 'number of cycles
c = 300 'initial weight hopper
a = 0.00001 'tablet weight
For n = 1 To 10000000
c = c - a 'one tablet is taken packaging machines
Next n
Text1.Text = c 'modified weight hopper
End Sub
In this example, the filling machine picked up from the hopper 100 kg of product, and the weight of products in the hopper has not changed. Next, bring the weight of the molding machine hopper to 500 kg and stop. Filling machine will take all the tablets from the hopper and also stops. The program will show the weight of 500kg in the bunker. Come running specialists, test sensors, wires, computer, and say that the program hung. But the program does not hang, it continues to run smoothly and every check will confirm this. Simply the number of 0.0001 hit in the cyclic hole and emerge from it can not.
As a result, we were lucky that it was a pharmaceutical plant, not the Sayan-Shushenskaya GES.
In fact, an experienced programmer would never make a cyclic subtraction (or summation) in this way.
This example is fictitious purpose, and so can not be considered, although in terms of mathematics are all flawlessly.
This error is typical of mathematicians and novice programmers.
I would say that the main work of the programmer is to struggle with errors, but not in the mathematical solution to the problem.
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
struct acc_comp {
float value;
float compens;
};
void
sub_compens(struct acc_comp *acc, float quantum)
{
float tmp, c;
tmp = quantum - acc->compens;
c = acc->value - tmp;
acc->compens = acc->value - c - tmp;
acc->value -= tmp;
}
void
sum_compens(struct acc_comp *acc, float quantum)
{
float tmp, c;
tmp = quantum - acc->compens;
c = acc->value + tmp;
acc->compens = c - acc->value - tmp;
acc->value += tmp;
}
void
sub_test()
{
struct acc_comp hopper;
struct acc_comp bunker;
float tablet;
int n, i;
n = 10000000;
hopper.value = 300.0;
hopper.compens = 0.0;
bunker.value = 0.0;
bunker.compens = 0.0;
tablet = 0.00001;
for (i = 0; i < n; i++)
{
sub_compens(&hopper, tablet);
sum_compens(&bunker, tablet);
}
hopper.value -= hopper.compens;
bunker.value += bunker.compens;
printf("Left in hopper: %04.5f kg\n", hopper.value);
printf("Held in bunker: %04.5f kg\n", bunker.value);
}
int
main(int argc, char *argv[])
{
sub_test();
return 0;
}
The preceding example is taken from real industrial package.
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
float bunker, bunker1, tablet, tablet1, compens;
long int n, i;
int
main(int argc, char *argv[])
{
tablet = 0.00001; /* tablet weight */
tablet1 = 0.0; /* tablet weight in view of errors in previous iterations */
bunker = 300.0; /* initial weight hopper */
bunker1 = 0.0; /* weight of the hopper after the next iteration */
compens = 0.0; /* compensation weight loss pills */
n = 10000000; /*number of cycles */
for (i = 0; i < n; i++)
{
/* tablet weight-compensated error */
tablet1 = tablet - compens;
/*weight of the hopper after deducting compensated tablets*/
bunker1 = bunker - tablet1;
/* calculation of compensation for the next iteration */
compens = (bunker - bunker1) - tablet1;
/*new weight hopper */
bunker = bunker - tablet1;
}
printf("Bunker: %04.5f kg\n", bunker);
return 0;
}
As can be seen from this example, the programmer has to calculate the error of the result in each cycle, to account for it in the next cycle. When computer calculations can distinguish two types of rounding:
1. The result of arithmetic operation is always rounded.
2. Output and input of a real number in the box Windows is rounded.
In the first case, the variable is rounded to one of 4 types of rounding IEEE754, the default rounding occurs to the nearest integer.
In this case, the variable receives a new rounded value.
In p.9.2 we considered the addition of two identical numbers:
1. Addition with the same number (the error shift = 0.0).

Here the result of the addition of two numbers is absolutely accurate, but the result was rounded off by a microprocessor.
Thus, to the exact result has been added to rounding error. In general, the rounding error is within the accuracy of the numbers.
In the second case, the variable does not change its meaning, just in Windows window displays the rounded value of the real numbers.
It turns out that the original variable and displaying it in Windows is a different number.
This is not the fault of the format IEEE754, this is a bug Windows.
Single variable is displayed in the Windows 7 significant figures rounded to nearest whole number.
3DFCD6EA = +0,12345679104328155517578125 box is displayed as 0,1234568
For variables of type Double to a Windows box displays 15 significant digits rounded to the nearest whole number.
3FBF9ADD3746F67D = +0,12345678901234609370352046653351862914860248565673828125 displayed as 0.123456789012346
The question of how important variable when we enter into the window Windows 0,123456789012346?
This value will be equal to this number:
3FBF9ADD3746F676 = +0,1234567890123459965590058118323213420808315277099609375
That is, the value of 3FBF9ADD3746F67D we generally can not insert directly into the program code.
But we can cheat and paste into the x = 0.123456789012346 +1 E-16.
The resulting variable will be equal to 3FBF9ADD3746F67D (this is used in the example of dirty zero)
Display or to a PC through the window is a number impossible.
As a result of action arises Windows a number of unpleasant situations.
1. You do not have technical capability to display or enter the exact values ??of the variables in the windows, which in itself is very sad.
2. The emergence of serious errors, such as dirty zero.
"dirty zero" is when you or the program assumes that the variable is not equal to zero - zero
Dim a As Double
'nulling the apparent magnitude
Private Sub Command1_Click()
Dim b As Double
Dim c As Double
b = Val(Replace(Text2.Text, ",", "."))
c = a - b
Text3.Text = c
End Sub
Private Sub Form_Load()
'Enter the number of 3FBF9ADD3746F67D
a = 0.123456789012346 + 1E-16
Text1.Text = a
End Sub
The result of the program in the above example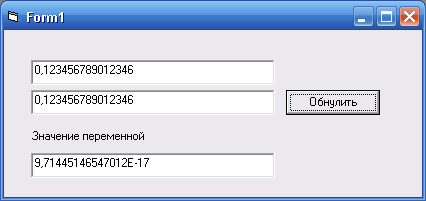
As a result, a variable that the operator considers zero - zero is not equal
Relative error of the result is infinity.
In the logical comparison operations that are not zero may divert program execution to another branch of the algorithm.
These errors occur when working with numbers located on the border of the normalized / denormalized number representation.
They are associated with differences in the representation of numbers in IEEE754 format and transfer the difference formulas in IEEE754 format real numbers.
That is, the device (or software) should use different algorithms depending on the position of a real number on a number line format.
In addition, it leads to a complication of devices and algorithms, there are still uncertainties of the transition zone.
The uncertainty of the transition zone is that the standard does not define a specific value of the transition boundary.
In essence, the transition boundary is between two real numbers:
The last denormalized number 000FFFFFFFFFFFFF:
Accurate decimal value of this number:
+2,2250738585072008890245868760858598876504231122409594654935248025624400092282356951787758888037591552642309780950
4343120858773871583572918219930202943792242235598198275012420417889695713117910822610439719796040004548973919380791
9893608152561311337614984204327175103362739154978273159414382813627511383860409424946494228631669542910508020181592
6642134996606517803095075913058719846423906068637102005108723282784678843631944515866135041223479014792369585208321
5976210663754016137365830441936037147783553066828345356340050740730401356029680463759185831631242245215992625464943
0083685186171942241764645513713542013221703137049658321015465406803539741790602258950302350193751977303094576317321
0852507299305089761582519159720757232455434770912461317493580281734466552734375e-308
and the first normalized number 0010000000000000:
Accurate decimal value of this number:
+2,2250738585072013830902327173324040642192159804623318305533274168872044348139181958542831590125110205640673397310
3581100515243416155346010885601238537771882113077799353200233047961014744258363607192156504694250373420837525080665
0616658158948720491179968591639648500635908770118304874799780887753749949451580451605050915399856582470818645113537
9358049921159810857660519924333521143523901487956996095912888916029926415110634663133936634775865130293717620473256
3178148566435087212282863764204484681140761391147706280168985324411002416144742161856716615054015428508471675290190
3161322778896729707373123334086988983175067838846926092773977972858659654941091369095406136467568702398678315290680
984617210924625396728515625e-308
Since the boundary is a real number, its precision can be set to infinity and digital device or program
may not have the bit for a decision to include some range of the number.
From the above it is clear that the view that the floating-point result is not beyond the relative error in reporting the greatest number is false. Errors listed in Item 9 are added together. Such errors as dirty and dangerous zero reduction can make calculation errors unacceptable. Particular attention in the programming of computer calculations the programmer should be paid to the results close to zero.
Some experts believe that the format of numbers represents a threat to humanity.
You can read about it in the article IEEE754-tick threatens mankind
Although many of the facts in this article over-dramatized, and possibly misinterpreted, but the problem is computing correctly reflected philosophically.
I'm not a dramatization of the calculations on the standard IEEE754. Standard operating since 1985 and fully entered into the standard IEEE754-2008, which broadened the accuracy of calculations. However, the problem of reliability computing today is very urgent, and the standard IEEE754-2008 and ISO recommendations have not solved this problem. I think in this area needed an innovative idea that developers Standard IEEE754-2008 unfortunately do not possess.
Innovative ideas usually come from.
The main innovative ideas in our world were made by amateurs (like-minded people not for money).
A striking example of this situation was the invention of the phone.
When a school teacher Alexander Graham Bell (Alexander Graham Bell) came up with a patent for an invention of the telephone to the president of telecommunications company Western Union Company,
which is owned by the transatlantic cable connection with an offer to buy his patent for the invention of the telephone, he was not expelled - no.
The president of that company offered to consider this question the advice of experts in the field of telegraphy, consisting of specialists and scholars in the field of telecommunications.
Experts gave their opinion that this invention is useless in the field of telecommunications and it is futile.
Some experts have even written a report that it tsirkachestvo and charlatanism!
Alexander Graham Bell, along with his father in law, decided independently to promote his invention.
After about 10 years, the telecommunications giant Western Union Co., was virtually eliminated phone business from the sphere of telecommunication technologies.
Today you can see in many Russian cities windows that says Western Union, this company which is engaged in transferring money around the world, and once she was the international telecommunications giant.
We can conclude: opinions of experts in innovative technologies are useless!
If you think that since the invention of the telephone (1877) in people's minds that something has changed, you're wrong.
If scientists (who are inventing new) and professionals (who know how to use the well-known) can not solve the problem, you need innovation.
Links to new ideas in the field of representation of real numbers in hardware:
1. Approksimetika
2. ....?< br>
If you know of other innovative ideas in the field of representations of real numbers, then we will be happy to get links to these sources.
I would suggest to represent real numbers as fixed-point.
To view the full range of numbers Double enough to have a variable consisting of 1075 bits integer part and 1075 bits of fractional part, ie about 270 bytes per variable.
In this case, all numbers will be presented with the same absolute accuracy.
You can work with numbers in the entire range the real axis, that is, it becomes possible to summarize large numbers of small numbers.
Step numbers on the real axis is uniform, that is the real axis is linear.
The data type will be only one, ie do not need the whole, real and other types.
Here the problem is the realization of registers of microprocessors dimension of 270 bytes, but it's not a problem for modern technology.
To write p.9 I had to create a program that represents a number as a variable to a fixed point, long 1075.1075 bytes.
Where the number can be represented as a string of characters ASCII, ie one symbol equals one digits.
Just had to write all the arithmetic operations with strings ASCII.
This program is similar to a paper calculation. Since mathematical ability microprocessor in it are not used, she said slowly.
Why I did it?
I could not find a program that could accurately represent the number of IEEE754 format, in decimal form.
I also did not find the program (although they certainly have what no doubt) where you can enter in box 1075 of significant decimal digits.
Here for example just the decimal value of the number of double 7FEFFFFFFFFFFFFF:
+17976931348623157081452742373170435679807056752584499659891747680315726078002853876058955
863276687817154045895351438246423432132688946418276846754670353751698604991057655128207624
549009038932894407586850845513394230458323690322294816580855933212334827479782620414472316
8738177180919299881250404026184124858368,0
You can use the IEEE754 v.1.0
to study and evaluate the errors when working with real numbers given in the format of IEEE754.
References:
1. IEEE Standard for Binary Floating-Point Arithmetic. Copyright 1985 by The Institute of Electrical and Electronics Engineers, Inc 345 East 47th Street, New York, NY 10017, USA
Acknowledgments:
Sitkarevu Grigory(sitkarev@komitex.ru, sinclair80@gmail.com). For assistance in creating an article.
Archive of reviews with comments View (Send us feedback on the e-mail: info@softelectro.ru)